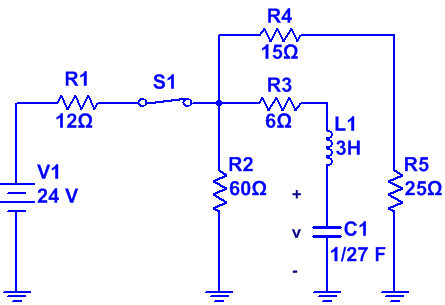
Ej8. El interruptor del circuito de la figura ha estado cerrado durante un largo período de tiempo, en el instante t = 0, se abre:
Obtener la evolución de v(t).
Vamos a analizar el circuito, dado por el enunciado del problema, alrededor del instante t = 0, que es cuando se produce un cambio del interruptor.
· t < 0: Interruptor cerrado durante un largo período de tiempo.
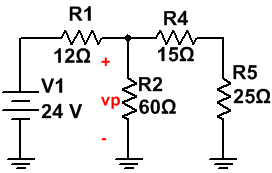
El circuito ha estado durante un largo período de tiempo con el interruptor cerrado, por lo que el condensador se comportará como un circuito abierto y el inductor como un corto circuito.
El circuito que tenemos es el siguiente:
Obtenemos su equivalente:
Donde:
· Req1 = R2 || (R4 + R5) = [60· (15 + 25)]/(60 + 15 + 25) = 24 Ω
La evolución de la tensión requerida es fácil, empleamos un divisor de tensión:
· vp = VC1p = [Req1/(Req1 + R1)]·V1 = [24/(24 + 12)]·24 = 16 V
Y el inductor, estará descargado totalmente:
· IL1p = 0 A
Ahora, pasamos a estudiar el circuito en el instante t = 0.
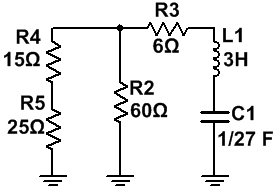
· t = 0: Interruptor abierto.
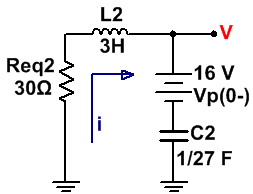
El circuito que tenemos es el siguiente:
Simplificamos:
Donde:
· Req2 = R3 + [R2 || (R4 + R5)] = Req1+ R3 = 24 + 6 = 30 Ω
Cuando tenemos elementos cargados, como en este caso, podemos dibujar el circuito equivalente en función de dichos elementos:
· Condensador: Un condensador sin polaridad y de la misma capacidad pero sin ninguna carga inicial, con una fuente de tensión lineal en serie de valor y polaridad a la carga inicial del condensador.
· Inductor: Un inductor del mismo valor pero sin ninguna carga inicial, con una fuente de corriente lineal en paralelo de valor y polaridad a la carga inicial del inductor.
Por lo tanto, teniendo en cuenta dichas premisas, el circuito que tenemos es el siguiente:
· NOTA: Tanto el condensador C2 cómo el inductor L2 es de la misma capacidad e inductancia respectivamente, que el condensador inicial del circuito (C1) y la inductancia inicial del circuito (L1), pero no tiene la misma polaridad, aparte, el condensador no tiene ninguna carga inicial, es por ello, que al no ser el mismo (ya que hemos empleado las condiciones de equivalencia para cuando existen elementos cargados), se ha nombrado cómo: C2 y L2.
En estas condiciones, tenemos dos comportamiento en el circuito, por un lado: El régimen transitorio (vn) y por el otro: El régimen permanente (vp). La solución general será del tipo:
· v(0+) = vp + vn
Así que vamos a obtener los dos por separado.
· Régimen Permanente:
Este caso, el circuito ha estado en la configuración presentada, durante un largo período de tiempo, tanto el condensador cómo el inductor se descargarán.
Por lo que, los datos que tendremos son:
· vp = 0 V.
Y evidentemente, la carga de ambos elementos serán nulas ya que se descargarán:
· VC2p = 0 V
· iL2p = 0 A
· Régimen Transitorio:
El condensador se irá descargando, realizamos el análisis mediante LVK:
· [Ec1] VReq2 + VL2 + v = 0
Donde:
· VReq2 = i·Req2
· VL2 = L2Di
· v = Vp(0- ) + VC2
Sustituimos en [Ec1]:
· [Ec2] i·Req2 + L2Di + Vp(0- ) + VC2 = 0
Donde:
· i = iC2 = iL2
· VC2 = vn - Vp(0- )
· iC2 = C2D(vn - Vp(0- ))
Sustituimos en [Ec2]:
· Req2·C2D(vn - Vp(0- )) + C2·L2D2 (vn - Vp(0- )) + Vp(0- ) + vn - Vp(0- ) = 0
Simplificamos:
· Req2·C2Dvn + C2·L2D2 vn + vn = 0
Reordenamos y dividimos por C2·L2:
· [Ec3] D2 vn + Dvn·(Req2/L2) + (1/L2·C2)·vn = 0
Ya tenemos nuestra ecuación diferencial homogénea de 2º Orden, que sabemos que debe ser del tipo:
· s2 + 2α·s + w20 = 0
Y en este caso, los parámetros α y w0 son:
· Factor de amortiguamiento ≡ α = Req2/2L2 = 30/(2·3) = 5 s-1
· Frecuencia natural ≡ w0 = √[ (1/L2·C2)] = √[ (1/3·(1/27))] = 3 rad/s
Y teniendo el valor de estos dos parámetros, podemos determinar cual es el comportamiento de nuestro circuito. En nuestro caso:
· α > w0
Al ser la frecuencia natural menor que el factor de amortiguamiento, el comportamiento de nuestro circuito es: Respuesta Sobreamortiguada, cuya solución a la respuesta homogénea es:
· vn(t) = k1·es1·t + k2·es2·t
Dónde:
· s1 = - α + (α2- w20)1/2 = - 5 + (52- 32)1/2 = - 1
· s2 = - α - (α2- w20)1/2 = - 5 - (52- 32)1/2 = - 9
Por lo tanto, la solución completa es, la compuesta por la respuesta permanente más la respuesta transitoria:
· v(t) = vp + vn = 0 + k1·e-t + k2·e-9t = k1·e-t + k2·e-9t
Ya tenemos la estructura de cómo será la evolución de la tensión requerida para este instante de tiempo. Nos falta, obtener los valores de los parámetros.
Para ello, vamos a aplicar las condiciones iniciales de los componentes que forman nuestro circuito.
· Inductor:
Al estar los elementos en serie, a todos le atraviesa la misma intensidad:
· iL2 = iC2
Donde:
· iC2 = C2D(v(t) - Vp(0- )) = C2Dv(t)
Obtenemos la primera derivada de la tensión v(t):
· Dv(t) = - k1·e-t - 9k2·e-9t
Y teniendo en cuenta la condición del inductor:
· iL2(t-) = iL2(t+)
En el instante t = 0:
· iL2(0) = 0 A
· Dv(0) = - k1·e-0 - 9k2·e-9·0 = - k1 - 9k2
El inductor L2 está totalmente descargado, por lo tanto, en el instante t = 0:
· 0 = C2·[- k1 - 9k2]
Por lo tanto, tenemos la primera ecuación con dos incógnitas:
· [ExpI] k1 + 9k2 = 0
Pasamos a evaluar las condiciones iniciales del condensador para obtener la segunda expresión necesaria.
· Condensador:
Al tener el circuito equivalente del comportamiento de los elementos cargados, vamos a analizarlo. Volvemos a realizamos un análisis de LVK:
· [Ec1] VReq2 + VL2 + v = 0
Donde:
· VReq2 = i·Req2
· VL2 = L2Di
· v = Vp(0- ) + VC2
Sustituimos en [Ec1]:
· [Ec2] i·Req2 + L2Di + Vp(0- ) + VC2 = 0
Donde:
· i = iC2 = iL2
· iC2 = C2D(v(t) - Vp(0- ))
Sustituimos en [Ec2]:
· Req2·C2D(v(t) - Vp(0- )) + C2·L2D2(V(t) - Vp(0- )) + Vp(0- ) + VC2= 0
Simplificamos:
· Req2·C2Dv(t) + C2·L2D2v(t) + Vp(0- ) + VC2 = 0
Reordenamos la expresión dividiendo por C2·L2:
· [Ec4] D2v(t) + (Req2/L2)Dv(t) = - (Vp(0- ) + VC2)/(C2·L2)
Obtenemos la primera y segunda derivada de la tensión v(t):
· Dv(t) = - k1·e-t - 9k2·e-9·t
· D2v(t) = k1·e-t + 81k2·e-9·t
Teniendo en cuenta la condición que debe cumplir el condensador:
· VC2(t- ) = VC2(t+ )
En el instante t = 0:
· VC2(0- ) = 0 V
· Dv(0) = - k1·e-0 - 9k2·e-9·0 = - k1 - 9k2
· D2v(0) = k1·e-0 + 81k2·e-9·0 = k1 + 81k2
Sustituimos en [Ec4]:
· k1 + 81k2 + (Req2/L2)·(- k1 - 9k2) = - Vp(0- )/(C2·L2)
Sustituimos por los valores de los elementos implicados y obtenemos la segunda expresión:
· [ExpII] k1 + k2 = 16
Ya tenemos las dos ecuaciones con dos incógnitas:
· [ExpI] k1+ 9k2 = 0
· [ExpII] k1 + k2 = 16
Resolvemos, ya sea mediante Gauss o cambiando la variable de una ecuación a otra, y obtenemos los siguiente valores para los parámetros requeridos:
· k1 = 18
· k2 = - 2
Ya hemos obtenido ambos parámetros, por lo que, una expresión para la tensión requerida es:
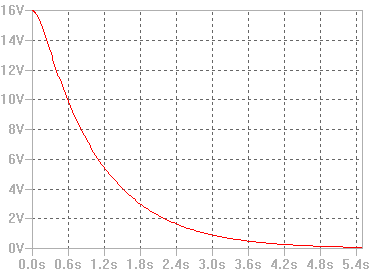
· v(t) = 18·e-t - 2·e-9t, t ≥ 0
Por lo tanto, en modo resumen, una expresión para la evolución de la tensión , dadas las condiciones que nos expone el enunciado del problema, es:
Cuya representación gráfica es:
Os dejo una simulación realizada en LTSpice:
| Problema 8: Transitorios de 2º Orden | |||||||||
|


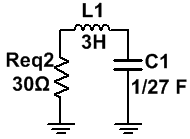










0 comentarios:
Publicar un comentario