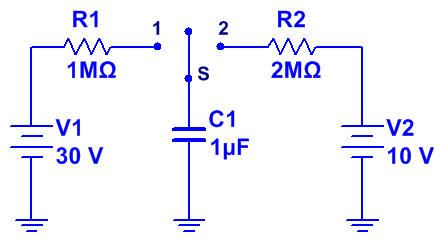
Ej9. En el instante t = 0, el interruptor S se conecta al terminal 1 y permanece en esta posición hasta que la tensión en el condensador alcanza 20 V. A continuación, el interruptor pasa al terminal 2 y permanece en dicha posición hasta que la tensión del condensador alcanza los 15 V.
En dicho momento, el interruptor pasa a la posición de abierto (no está ni el la posición 1 ni el la 2).
Obtener:
a) La evolución de la tensión del condensador.
b) La evolución de la intensidad que atraviesa al condensador.
c) Energía consumida en los resistores.
Apartado a)
Este problema es un poco peculiar, ya que no nos dicen los intervalos de cambio de estado del interruptor sino que, nos dan las pistas necesarias (a través de la tensión que llega a alcanzar al condensador) de dichos cambios.
Por lo tanto, debemos obtener dichos instantes de tiempo donde el interruptor cambia de una posición a otra.
Para empezar, asumimos que el condensador (antes de pasar el interruptor a la posición 1) está completamente descargado, ya que el enunciado del problema nos nos indica nada al respecto.
Bien, vamos a empezar a analizar que es lo que sucede cuando el interruptor pasa a la posición 1.
· t = 0. S posición 1:
¡Ojo! Hay que tener en cuenta que el interruptor está en esta posición hasta que la tensión del condensador sea de 20 V.
El circuito que tendremos será el siguiente:
Para este caso, tenemos dos comportamiento en el circuito, por un lado: El régimen transitorio (vn) y por el otro: El régimen permanente (vp). La solución general será del tipo:
· v(0+) = vp + vn
Así que vamos a obtener los dos por separado.
· Régimen Permanente:
Este caso, el interruptor S permanece en la posición 1 durante un largo período de tiempo, por lo que, el condensador se cargará completamente y se comportará como un circuito abierto.
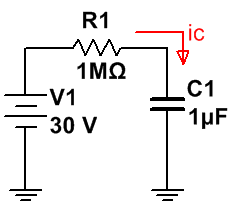
El circuito que tenemos es el siguiente:
Obtener la tensión del condensador es fácil, es la misma fuente de tensión lineal:
· vp = V1 = 30 V.
El condensador se cargará hasta la tensión máxima que proporciona el circuito, en este caso, hasta 30 V.
· Régimen Transitorio:
Realizamos el análisis mediante LVK:
· [Ec1] vn + ic·R1 - V1 = 0
Dónde:
· ic = C·Dvn
Sustituimos el valor en [Ec1] y dividimos por C:
· Dvn + [1/(C1·R1)]·vn = V1/(C1·R1)
Ya tenemos nuestra ecuación diferencial de 1º Orden, la ecuación homogénea es:
· [Ec2] Dvn + [1/(C1·R1)]·vn = 0
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· vn(t) = k·e-A·t
Realizamos la primera derivada y sustituimos en [Ec2]:
- k·A·e-A·t + [1/(C1·R1)]·k·e-A·t = 0
Analizamos en circuito en el instante t = 0, por lo tanto:
- k·A + [1/(C1·R1)]·k = 0
Despejamos el parámetro A:
· A = 1/(C1·R1) = 1/(1·106 · 1·10-6) = 1 s-1
Por lo tanto, la constante de tiempo en el instante t = 0 es:
· τ = 1/A = 1/1 = 1 s
Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del condensador.
· Condensador: La tensión no puede cambiar bruscamente en un instante concreto.
Hay que tener en cuenta que el condensador está completamente descargado:
· v(0-) = 0 V
En el instante t = 0:
· v(0-) = v(0+)
Por lo tanto:
· 0 = vp + vn = 30 + k·e-t = {t = 0} = 30 + k
Despejamos k:
· k = - 30
Así que, una expresión para la tensión del condensador es:
· v(t) = 30 - 30·e-t = 30·(1 - e-t)
¡Cuidado! Lo vuelvo a repetir, el interruptor cambia de posición (de la 1 hasta la 2) cuando el condensador tenga una tensión de 20 V, por lo que debemos calcular dicho instante:
· v(t) = 30·(1 - e-t) = 20
Despejamos:
· e-t = - (20/30) + 1 = 1/3
Aplicamos logaritmo neperiano en ambas partes de la igualdad:
· - t = ln(1/3)
Por lo tanto, el instante que el interruptor cambia desde la posición 1 hasta la 2 es:
· t ≈ 1.098612 s
Esto quiere decir que en el instante, aproximadamente 1.098612 s, el interruptor cambia desde la posición 1 hasta la posición 2.
Ahora, ya podemos exponer la condición en las que se cumple nuestra expresión matemática para la tensión del condensador en las circunstancias dadas:
· v(t) = 30·(1 - e-t), 0 < t < 1.098612 s
Ya estamos en disposición de cambiar nuestro interruptor a la posición 2.
· t = 1.098612 s. S posición 2:
Antes de entrar en materia, hay que tener en mente que el interruptor cambiará al estado inicial (sin estar en ningún terminal) cuando la tensión del condensador sea de 15 V.
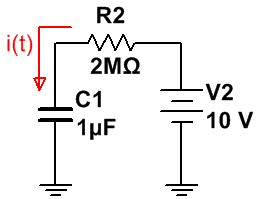
El circuito que tendremos será el siguiente:
Para este caso, al igual que antes, tenemos dos comportamiento en el circuito, por un lado: El régimen transitorio (vn) y por el otro: El régimen permanente (vp). La solución general será del tipo:
· v(1.098612+) = vp + vn
Así que vamos a obtener los dos por separado.
· Régimen Permanente:
Este caso, el interruptor S permanece en la posición 2 durante un largo período de tiempo, por lo que, el condensador se cargará completamente y se comportará como un circuito abierto.
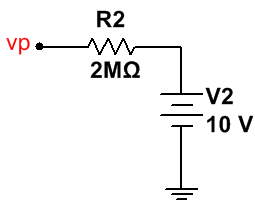
El circuito que tenemos es el siguiente:
Obtener la tensión del condensador es fácil, es la misma fuente de tensión lineal:
· vp = V2 = 10 V.
El condensador se cargará hasta la tensión máxima que proporciona el circuito, en este caso, hasta 10 V.
· Régimen Transitorio:
Realizamos el análisis mediante LVK:
· [Ec3] vn + ic·R2 - V2 = 0
Dónde:
· ic = C·Dvn
Sustituimos el valor en [Ec3] y dividimos por C:
· Dvn + [1/(C1·R2)]·vn = V2/(C1·R2)
Ya tenemos nuestra ecuación diferencial de 1º Orden, la ecuación homogénea es:
· [Ec4] Dvn + [1/(C1·R2)]·vn = 0
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· vn(t) = k·e-A·(t - 1.098612)
Realizamos la primera derivada y sustituimos en [Ec4]:
- k·A·e-A·(t - 1.098612) + [1/(C1·R2)]·k·e-A·(t - 1.098612) = 0
Analizamos en circuito en el instante t = 1.098612 s, por lo tanto:
- k·A + [1/(C1·R2)]·k = 0
Despejamos el parámetro A:
· A = 1/(C1·R2) = 1/(1·10-6 · 2·106) = 0.5 s-1
Por lo tanto, la constante de tiempo en el instante t = 1.098612 s es:
· τ = 1/A = 1/0.5 = 2 s
Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del condensador.
· Condensador: La tensión no puede cambiar bruscamente en un instante concreto.
Hay que tener en cuenta que el condensador no está descargado:
· v(1.098612-) = 20 V
En el instante t = 1.098612 s:
· v(1.098612-) = v(1.098612+)
Por lo tanto:
· 20 = vp + vn = 10 + k·e-0.5·(t - 1.098612) = {t = 1.098612 s} = 10 + k
Despejamos k:
· k = 20 - 10 = 10
Así que, una expresión para la tensión del condensador es:
· v(t) = 10 + 10·e- 0.5·(t - 1.098612) = 10·(1 + e- 0.5·(t - 1.098612))
¡Cuidado! Lo vuelvo a repetir, el interruptor cambia de posición (en ningún terminal) cuando el condensador tenga una tensión de 15 V, por lo que debemos calcular dicho instante:
· v(t) = 10·(1 + e- 0.5·(t - 1.098612)) = 15
Despejamos:
· e- 0.5·(t - 1.098612) = (15/10) - 1 = 0.5
Aplicamos logaritmo neperiano en ambas partes de la igualdad:
· - 0.5(t - 1.098612) = ln(0.5)
Por lo tanto, el instante que el interruptor cambia a su estado inicial (no está conectado a ningún terminal):
· t = - [ln(0.5)]/0.5 + 1.098612 ≈ 2.484906 s
Esto quiere decir que en el instante, aproximadamente 2.484906 s, el interruptor cambia a la posición inicial (sin estar conectado a ningún terminal).
Ahora, ya podemos exponer la condición en las que se cumple nuestra expresión matemática para la tensión del condensador en las circunstancias dadas:
· v(t) = 10·(1 + e- 0.5·(t - 1.098612)), 1.098612 < t < 2.484906 s
En modo resumen, la expresión matemática o la evolución de la tensión del condensador dadas las circunstancias dadas es la siguiente:
Cuya representación gráfica es la que se muestra a continuación:

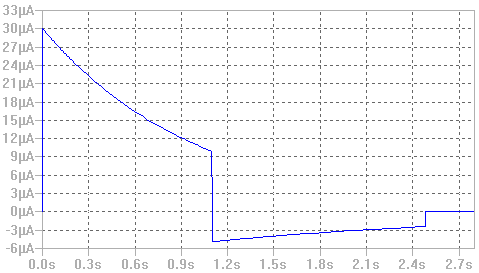
Apartado b)
En este apartado nos piden obtener la evolución de la corriente que atraviesa al condensador, por propia definición, sabemos que la intensidad de un condensador viene expresado por la siguiente expresión matemática:
· i(t) = C·Du(t)
Dónde tenemos ya calculado la tensión de dicho condensador (obtenida en el apartado anterior), por lo tanto, simplemente, realizamos la derivada para obtener la solución a este apartado:
Cuya representación gráfica es la que se muestra a continuación:
Apartado c)
En este apartado, nos piden obtener la energía consumida por ambos resistores, por definición:
· w(t) = ʃp(t)·dt
En nuestro caso, tenemos la expresión de la intensidad obtenida en el apartado anterior, por lo que:
· w(t) = ʃ(i2·R)·dt
Vamos a obtener la energía consumida para cada resistor.
· Resistor 1:
Hay que tener en cuenta que este resistor está presente sólo en el instante: 0 < t < 1.098612 s
Por lo tanto, la energía consumida será de:
· Resistor 2:
Hay que tener en cuenta que este resistor está presente sólo en el instante: 1.098612 < t < 2.484906 s
Por lo tanto, la energía consumida será de:
Por lo tanto, la energía total consumida será la suma de ambas energías:
· wtotal = wR1 + wR2 = 4·10-4 + 3.75·10-5 = 437.5 μJ
Por lo tanto, la energía consumida por ambos resistores, dadas las condiciones del problema, es de 437.5 μJ.
· NOTA: No se han resuelto las integrales paso a paso ya que son inmediatas, aún así, si alguien necesita su resolución paso a paso, que lo comente por comentarios y se la proporcionaré.
Como alternativa, las integrales se pueden obtener mediante las calculadoras que en este blog exponemos o, mediante el programa wxMaxima, aquí su expresión:
>> wR1: integrate((3*10^-5*%e^(-t))^2*1*10^6, t, 0, 1.098612);
>> wR2: integrate((-5*10^-6*%e^(-0.5*(t-1.098612)))^2*2*10^6, t, 1.098612, 2.484906);
>> wtotal = wR1 + wR2
Os dejo una simulación realizada en LTSpice:
| Problema 9: Transitorios de 1º Orden | |||||||||
|




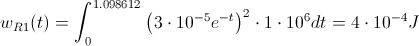
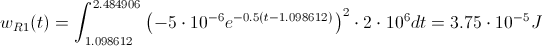








0 comentarios:
Publicar un comentario